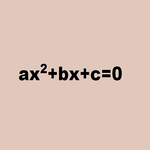
Lösen Sie jede Gleichung zweiten Grades (sowohl vollständige als auch unvollständige Gleichungen)
advertisement
| Name | Quadratic Equations Solver |
|---|---|
| Version | 1.2 |
| Aktualisieren | 28. Juni 2023 |
| Größe | 7 MB |
| Kategorie | Lernen |
| Installationen | 1Tsd.+ |
| Entwickler | Math applications |
| Android OS | Android 4.1+ |
| Google Play ID | com.mathapplications.seconddegreeequations |
Quadratic Equations Solver · Beschreibung
Der Benutzer kann jede Gleichung zweiten Grades lösen. Dazu müssen Sie die Werte der Koeffizienten a, b und c einsetzen. Wenn die Gleichung in Standardform vorliegt,
Koeffizient a ist die Zahl, die mit x zum Quadrat multipliziert wird, Koeffizient b ist die Zahl, die mit x multipliziert wird, und Koeffizient c ist der unabhängige Term.
Wenn die Koeffizienten a, b und c ungleich Null sind, ist die Gleichung zweiten Grades vollständig. In diesem Fall lösen wir die Gleichung mit der Formel.
Wenn jedoch b = 0 oder c = 0 ist, ist die Gleichung unvollständig und wir werden alternative Wege verwenden, um sie zu lösen.
Wenn b=0 ist, lösen wir die unvollständige Gleichung zweiten Grades wie eine Gleichung ersten Grades und berechnen am Ende die Quadratwurzel.
Wenn c=0, lösen wir die unvollständige Gleichung zweiten Grades mit der Faktorisierung und setzen jeden Faktor gleich Null.
Die Anwendung erklärt jeden Vorgang Schritt für Schritt.
Koeffizient a ist die Zahl, die mit x zum Quadrat multipliziert wird, Koeffizient b ist die Zahl, die mit x multipliziert wird, und Koeffizient c ist der unabhängige Term.
Wenn die Koeffizienten a, b und c ungleich Null sind, ist die Gleichung zweiten Grades vollständig. In diesem Fall lösen wir die Gleichung mit der Formel.
Wenn jedoch b = 0 oder c = 0 ist, ist die Gleichung unvollständig und wir werden alternative Wege verwenden, um sie zu lösen.
Wenn b=0 ist, lösen wir die unvollständige Gleichung zweiten Grades wie eine Gleichung ersten Grades und berechnen am Ende die Quadratwurzel.
Wenn c=0, lösen wir die unvollständige Gleichung zweiten Grades mit der Faktorisierung und setzen jeden Faktor gleich Null.
Die Anwendung erklärt jeden Vorgang Schritt für Schritt.







